東北大学 理学研究科物理学専攻
森田 克洋
本当は怖い磁性物理学
1.本当は怖いスピンハミルトニアン
磁性絶縁体のスピンハミルトニアンは近似的に以下のようになる。

第一項が交換相互作用、第二項がシングルイオン異方性、そして第三項がゼーマン項である。
ちなみに第三項のgiはよく言われるgテンソルのことである。たいていの場合は実対称行列になる。またgiなどのiの添え字は場所ごとに依存することを意味する。よってある位置にいる磁性イオンとまた別の位置にいる磁性イオンのgテンソルは違ってもよいのだ。これは物理学的に考えれば、クーロンポテンシャルなどが磁性イオンのいる場所によって違うのであれば当然のことである。シングルイオン異方性についても同様である。
このハミルトニアンは現在人気のキタエフ模型やそれに準ずる模型やXYZ模型(Jij行列が対角行列)、XXZ模型(Jij行列が対角行列でかつ1行1列と2行2列の成分が同じ値)、Heisenberg模型(Jij行列が対角行列で成分が全て同じ値)などこれら全ての模型を記述することが可能である。
では、ある物質を解析することを考えよう。このハミルトニアンの尋常じゃない自由度は結晶構造によって大幅に削減することが出来る。
例えば磁性原子のいる点(位置)にn回軸(nは2以上)が2つ存在し、かつお互いが直交していれば、eaiとebiの向きはその2つの軸方向になり、またgi行列の固有ベクトルがその2つの軸に対応する。またこれらはスピン軌道相互作用に大きく影響されるため近似的にはおおよそ配位子によって決定でき、結晶構造の対称性ではなく、配位子と磁性イオンのみの構造の対称性である程度推測はできそうだ。またそもそもS=1/2の場合は第2項を無視できる。(エネルギーがシフトするだけ)
結晶の任意の併進対称性や回転対称性、鏡映対称性などからJij行列もかなり限定される。
例えばもし磁性イオンがハニカム格子を形成しているが、結晶構造に6回軸(6回らせん軸ではない)があれば絶対に単純なキタエフ模型ではないと言えそうだ(例えば空間群がP6など)。これはキタエフ模型はどう考えても6回対称な構造ではないからである。
一方で3回回反軸と鏡映面を持っている場合はキタエフ模型になりうる(例えば空間群はR-3m, -3は本当は3の上にバーがのる。3回回反を意味する。)。より正確には第N隣接相互作用(Nは2以上)を無視すれば、必ず(?少し自信ないが)K-J-Γ-Γ’模型になる。
あるいは一般に、結晶中のi,jボンドの中心が反転対称性を有していればJijは実対称行列になる。これはDM相互作用が存在しないことと等価である。
このようにしてハミルトニアンの自由度を結晶構造によって大幅に落とすことが出来るのだが、残念ながらそれでもかなりの自由度が残っており、理論的にパラメータを決定するには尋常じゃないレベルの計算が要求される・・・かもしれない・・・。例外はいくつかあるだろうが、幸いスピン軌道相互作用が比較的小さく、電子軌道の縮退が無い場合はHeisenberg模型で十分ということはわかっている(本当?)が、それでも第二隣接相互作用などを十分な精度で決定することは大変であることに変わりはない。そして当然絶縁体でなければならない。
恐ろしい。
2.本当は怖いキュリー・ワイスの法則(Curie–Weiss law)
磁性体において最も基礎的で最も有名な法則の1つとしてキュリー・ワイス則があげられる。これは極めてシンプルであるにもかかわらず、ほとんどの磁性体に当てはまる法則である。
具体的には磁化率χは
となる。
ここでCはキュリー定数、θwはワイス温度である。
より具体的にはハミルトニアンを以下のようにする場合
Cとθwは次のようになる。
ここでNはサイト数である。また式(2)の第一項と式(4)の∑はボンド数個の和になるように定義する。
さらに具体的に、単純な第一隣接相互作用Jのみの1次元鎖では
θw = -2JS(S+1)/(3kB)
となる。
本題はここからである。
では式(1),(3),(4)は理論的にはどのような条件のときに成り立つのであろうか?
これはよく知られたように十分高温のときに成り立つ。
では十分高温とは何に比べてなのだろうか?あるいはどのくらい高温であるときなのであろうか?
これはワイス温度に比べて十分高温であればよい。
ではない。
なぜならば、例えば強磁性相互作用と反強磁性相互作用が混在していて、大きさ(絶対値)が等しい場合はワイス温度がゼロになりめちゃくちゃなことになる。
よって、最も絶対値が大きい交換相互作用に比べ十分大きい温度の場合に成り立つ。が正しい。
では絶対値が大きい交換相互作用に比べどのくらい温度が高ければいいのだろうか?
当然格子にもよるのであるが、私の経験上5~10倍くらい高くないと1%程度以上ズレてくる。
例えばS=1/2、真の交換相互作用JがJ=100K(正確にはJ/kB,以下では全てkBを省略)とし、温度Tが200K~300Kの範囲で無理やりキュリー・ワイス則によるフィッティングを行って交換相互作用を見積もると、大体30%程度大きく見積もれてしまう。(J~130Kと見積もられてしまう。)
・・・恐ろしい。
といっても信じられない人もいると思うので、Bonner-Fisher曲線などを使って自分で確かめてみよう!
当たり前であるが定量的な議論をする際は十分に注意する必要がある。
ではどうすればもっと精度よく交換相互作用などを見積もることが出来るだろうか?
これはよく知られた高温展開(級数展開)を利用すればよい。(あるいは対角化や有限温度ランチョス法やQMCなど)
実はキュリーワイス則は最低レベルのパデ近似+高温展開で得られる式と厳密に一致する。よって高温展開の次数を上げていけば精度は良くなっていく。
これは例えば簡単な数学でいえば
と
では後者の方が精度がいい(当たり前)ことに対応する。
そのため、磁化率の場合も同じで、キュリーワイス則を用いるよりも、より高次の高温展開などで得られた結果を用いる方が精度が高い(当たり前その2)。
さて、次は実験と比較する際の注意点である。
当然、実験では測定温度には限界があり、キュリーワイス則を満足する温度に到達しない場合が多い。さらに、十分高温に到達できたとしても実験で得られる磁化率は
となりχ0の影響を忘れてはいけない。(そんな人はいないはず)
このχ0は例えばヴァンブレック常磁性や原子(分子)の反磁性やサンプルフォルダーなどの反磁性などの和として与えられ温度に依存しない定数項として与えられる。
交換相互作用が大きい(例えばJ=200K)場合は式(5)は破綻しており、高温展開などで求めた磁化率を使って、g, J,χ0などをフィッティングパラメータとして決定しなければならない。(頑張ろう。)
では今度は逆に交換相互作用が十分小さい(例えばJ=1K)場合はどうだろうか?
当然T=200K~300K程度では式(5)は十分な精度であり、T=200K~300K程度の範囲で実験結果をフィッティングすることによって簡単に精度よく定量的にJ、g、χ0を求めることができる。
・・・本当にそうなのであろうか?
実はJもgも厳密には僅かに温度に依存する。それに伴ってχ0もわずかに温度に依存する。(χ0は温度に依存しないって言ったな。あれは嘘だ!)
その影響で(低温での)真の値はJ=1Kであるにもかかわらず、フィッティングによって求められた結果はJ=0.5Kだとか下手するとJ=-0.5Kだとか得られてしまっても不思議ではない。もはや符号すら正しく見積もれない可能性だってありうる。
・・・恐ろしすぎる。
ではどうすればいいのだろうか?
フィッティングする温度を下げてやればよい。(そして式(5)を使わなければなおよい。)
最後に一言
交換相互作用やg値を見積もることに成功しているのに、ワイス温度を見積もる意義は何なのだろうか?
見積もられたJやg値を式(3),(4)に代入してワイス温度やキュリー定数を求めるならまだわかるのだが・・・。もちろん言うまでもなく式(2)がその物質の正しいハミルトニアンかどうかも重要である。






3.本当は怖い磁化プラトー
量子スピン系の研究テーマの一つとして“磁化プラトー”があげられる。
これは絶対零度あるいは十分低温において,量子スピン系特有の量子現象であると考えられるため興味が持たれている。もちろん、イジングモデルなどの異方性が強い場合は古典系でも磁場の加える方向によっては磁化プラトーが出現するが、等方的なハイゼンベルグモデルでは量子スピン系でしか磁化プラトーは出現しない。さらに、フラストレーションがあればなおさら量子効果が顕著に現れ、磁化プラトーが出現しやすくなる。
・・・本当にそうなのであろうか?
もうここまで読んできた読者は察していると思われるが、
古典スピン系の等方的なハイゼンベルグモデルでフラストレーションが無くても絶対零度の磁化プラトーは出現する。
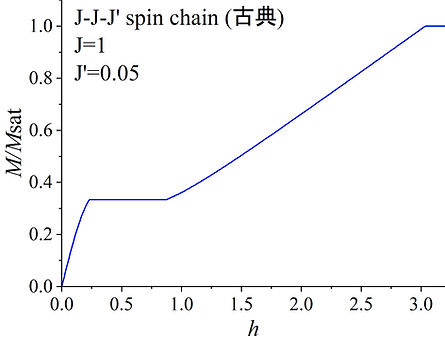
例えば1次元鎖で-J-J-J'-J-J-J'-・・・と3倍周期を持つモデルではJ’が小さければ1/3プラトーが出現する。当然単なる一次元鎖なのでフラストレーションは存在しない。
結果は図の通りである。
ちなみにプラトー上の磁気構造は-up-down-up-up-down-up-・・・構造である。
実験でもプラトーが観測されたらかと言って安易に”これは量子効果だ!”などと言ってはいけない。
以下営業
実験で得られた結果が古典スピン系でも存在しうる磁化プラトーなのか、それとも量子スピン系特有の磁化プラトーなのかをはっきりさせたい方がいましたら直接私にメールください(メール以外でもOK)。対応できそうであれば対応します。